The height of this triangle would be 10.4
In order to find this, you first must find the length of the sides. Using a manipulated formula for area of an equilateral triangle, we can determine the lengths of the side. Below if the formula.
S =
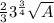
In this, S is the length of the side and A is the area. So we plug in and get:
S =
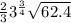
S =
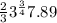
S = 12
Now that we have the side as 12, we can use the Pythagorean Theorem to find the height. If you split a equilateral triangle down the middle, you are left with two right triangles. Using this right triangle, the hypotenuse would be 12, the first leg would be 6 (half of the base) and the height would be the other leg. So we plug in and solve.
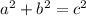
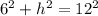
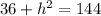
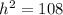
h = 10.4