Answer:
Option B)
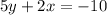
Explanation:
We are given the following information in the question:
Given equation of line:
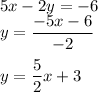
Comparing to the slope intercept form:
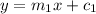
we get,
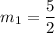
A line perpendicular will have a slope
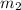 such that
such that
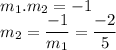
The equation of line is given by:
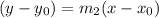
where
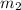 is the slope of line and
is the slope of line and
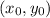 is a point through which the line passes. It is given that the line passes through the point (5, −4).
is a point through which the line passes. It is given that the line passes through the point (5, −4).
Putting all the values we get,
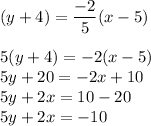
is the required equation of line.
Hence option B) is the correct answer.