Question

Which equations represent the line that is perpendicular to the line 5x − 2y = −6 and passes through the point (5, −4)? Check all that apply.

y = –x – 2
2x + 5y = −10
2x − 5y = −10
y + 4 = –(x – 5)
y – 4 = (x + 5)

Answer 1

Option B)
`5y + 2x = -10`

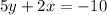
Explanation:

We are given the following information in the question:

Given equation of line:

`5x-2y =-6\\y = \displaystyle(-5x-6)/(-2)\\\\y = (5)/(2)x + 3`

Comparing to the slope intercept form:

`y = m_1x +c_1`

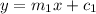
we get,
`m_1 = \displaystyle(5)/(2)`

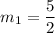
A line perpendicular will have a slope
`m_2` such that

`m_1.m_2 = -1\\m_2 = \displaystyle(-1)/(m_1) = (-2)/(5)`

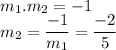
The equation of line is given by:

`(y-y_0) = m_2(x-x_0)`

where
`m_2` is the slope of line and
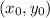`(x_0,y_0)` is a point through which the line passes. It is given that the line passes through the point (5, −4).

Putting all the values we get,

`(y +4) = \displaystyle(-2)/(5)(x-5)\\\\5(y+4) = -2(x-5)\\5y + 20 = -2x + 10\\5y + 2x=10-20\\5y + 2x = -10`

is the required equation of line.

Hence option B) is the correct answer.

Answer 2

Find the slope of the line first:
5x - 2y = -6,
y = (5/2)x + 3;
Since we need a line that's perpendicular, m = - (2/5).

The only equation that has the slope of this m is 2x + 5y = -10;