Question

The​ equation, with a restriction on​ x, is the terminal side of an angle theta in standard position. y= -2x Quadrant IV.

Give the exact values of the six trigonometric functions of theta. Select the correct choice below and fill in any answer boxes within your choice.

Answer 1

yes

Explanation:

sin(θ) =

✔ -15/17

cos(θ) =

✔ 8/17

tan(θ) =

✔ -15/8

csc(θ) =

✔ -17/15

sec(θ) =

✔ 17/8

cot(θ) =

✔ -8/15

Answer 2

In Q4, the terminal ray of our reference angle is the hypotenuse of the right triangle created by connecting the end of the terminal ray to the positive x-axis. Theta is the angle between these 2. In the equation, in the simplest form, if we sub in a 1 for x, then y = -2. That means the distance along the x axis (the base of the right triangle) is 1, and the height of the triangle is -2. We need now to find the measure of the hypotenuse using Pythagorean's Theorem.
`c^2=1^2+(-2)^2` and
`c^2=5` so
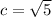
`c= √(5)`. The sin of theta is the ratio of the side opposite over the hypotenuse, so
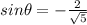
`sin \theta =- (2)/( √(5) )`, and
`csc \theta =- ( √(5) )/(2)`.
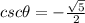
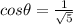
`cos \theta= (1)/( √(5) )` and
`sec \theta = ( √(5) )/(1)`.
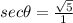
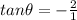
`tan \theta = -(2)/(1)` so
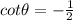
`cot \theta =- (1)/(2)`. There you go!