In Q4, the terminal ray of our reference angle is the hypotenuse of the right triangle created by connecting the end of the terminal ray to the positive x-axis. Theta is the angle between these 2. In the equation, in the simplest form, if we sub in a 1 for x, then y = -2. That means the distance along the x axis (the base of the right triangle) is 1, and the height of the triangle is -2. We need now to find the measure of the hypotenuse using Pythagorean's Theorem.
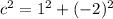
and
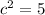
so
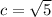
. The sin of theta is the ratio of the side opposite over the hypotenuse, so
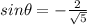
, and
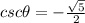
.
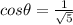
and
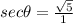
.
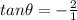
so
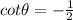
. There you go!