Question

Find a polar equation for the curve represented by the given cartesian equation. x2 + y2 = 10cx

Answer 1

The polar equation for the curve represented by the given cartesian equation is
`r=(10c)cos(\theta)`

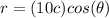
Explanation:

We were given the following equation:

`x^2+y^2=10cx`

and the relations between cartesian and polar coordinates are given by

`x=rcos(\theta)`

`y=rsin(\theta)`

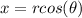
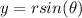
where r is a radius and θ an angle. Now we replace this relations in the original cartesian equation:

`(rcos(\theta))^2+(rsin(\theta))^2=(10c)rcos(\theta)\Leftrightarrow r^2cos^2(\theta)+r^2sin^2(\theta)=(10cr)cos(\theta)\Leftrightarrow r^2(cos^2(\theta)+sin^2(\theta))=(10cr)cos(\theta)`

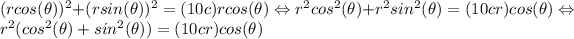
and we use that

`(cos^2(\theta)+sin^2(\theta))=1`

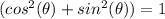
to simplify, then

`r^2=(10c)rcos(\theta)\Leftrightarrow r=(10c)cos(\theta)`

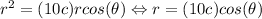
wich is the polar equation for the curve.

Answer 2

The usual rectangular to polar substitutions can be used:
x = r·cos(θ)
y = r·sin(θ)

These give
r² = 10c·r·cos(θ)
or
r = 10c·cos(θ)