Answer:
The polar equation for the curve represented by the given cartesian equation is
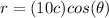
Explanation:
We were given the following equation:
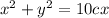
and the relations between cartesian and polar coordinates are given by
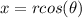
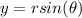
where r is a radius and θ an angle. Now we replace this relations in the original cartesian equation:
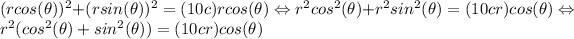
and we use that
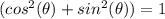
to simplify, then
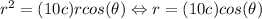
wich is the polar equation for the curve.