Question

A company sells mattresses for $365each. To produce a batch of nmattresses, there is a cost of $254 per mattress and a fixed or setup cost of $9,100 for the entire batch. Determine a function that gives the profit in terms of the number of mattresses produced. What is the number of mattresses that must be produced and sold in order for the company to break even

Answer 1

Any function to determine profit is revenue - cost.

If the number of mattresses made is x, then the revenue made per mattress is 365x.

Under the same assumption, the cost per mattress is 254x + 9100, adding the setup costs to the cost per mattress.

Thus, the function is
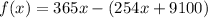
`f(x) = 365x - (254x + 9100)`. We can simplify this function.

First, lets expand the negative (the same as multiplying each value by -1).

`f(x) = 365x - 254x - 9100`

Next, we'll combine like terms.

`f(x) = 111x - 9100`
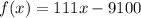
Therefore, the function for profit is
`f(x) = 111x - 9100`.

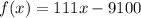
Continuing, we need to determine how many mattresses the company needs to break even. Breaking even means there is no profit, but also no loss. Otherwise, they make 0 total. So, we can set the function we just found to 0 and solve for x.


Set the function to 0.

`0 = 111x - 9100`

Add 9100 to both sides.

`9100 = 111x`

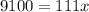
Divide both sides by 111.

`81.98 = x`

Rounding this number up, it would take 82 mattresses to break even.