Question

Find dy/dx when y = Ln (sinh 2x). A. 2 cosh 2x B. 2 sech 2x C. 2 coth 2x D. 2 csch 2x

Answer 1

The function given is a composite function. Let's work from the outside in:

`y=(ln(sinh(2x)))`

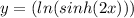
First step:

`(d)/(dx)[y]= (d)/(dx)[ln(sinh(2x))]`

Now, let's work it out:

`(dy)/(dx) = (1)/(sinh(2x) ) * (d)/(dx)[sinh(2x)]`

Next step:

`(dy)/(dx) = (1)/(sinh(2x) ) * cosh(2x) * (d)/(dx)[2x]`

Next step:

`(dy)/(dx) = (1)/(sinh(2x) ) * cosh(2x) *2`

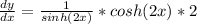
Simplify:

`(dy)/(dx) = (2cosh(2x))/(sinh(2x) )`

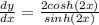
Simplify further:

`(dy)/(dx) = 2 ((cosh(2x))/(sinh(2x)))`

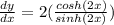
Remember that:

`{(cosh(x))/(sinh(x)) = coth(x)`

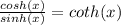
So, your final answer is: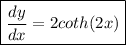

`\boxed{ (dy)/(dx) = 2coth(2x) }`

So, your answer is C. Hope I could help you!