The function given is a composite function. Let's work from the outside in:
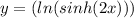
First step:
![(d)/(dx)[y]= (d)/(dx)[ln(sinh(2x))]](https://img.qammunity.org/2019/formulas/mathematics/high-school/x6yl6qurk3ihrh7vtcwe05e0ut9f72gv2t.png)
Now, let's work it out:
![(dy)/(dx) = (1)/(sinh(2x) ) * (d)/(dx)[sinh(2x)]](https://img.qammunity.org/2019/formulas/mathematics/high-school/i31rzsjfqogxtdsx4sqtw9wm75vxuthvgi.png)
Next step:
![(dy)/(dx) = (1)/(sinh(2x) ) * cosh(2x) * (d)/(dx)[2x]](https://img.qammunity.org/2019/formulas/mathematics/high-school/81258mehtkdwl5cyu9avtwifgzvpkaz389.png)
Next step:
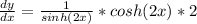
Simplify:
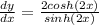
Simplify further:
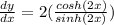
Remember that:
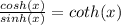
So,
your final answer is: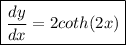
So, your answer is
C. Hope I could help you!