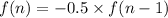Question

Which recursive formula can be used to generate the sequence shown, where f(1) = 9.6 and n > 1?

9.6, –4.8, 2.4, –1.2, 0.6, ...

Answer 1

The correct answer is f(n + 1) = –0.5f(n) since n is greater than 1

Answer 2

`f(n)=-0.5* f(n-1)`

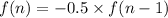
Explanation:

Sequence: 9.6, –4.8 , 2.4, –1.2, 0.6, ...

So, f(1) = first term = 9.6

r = common ratio =
`(-4.8)/(9.6) =(2.4)/(-4.8) = -0.5`

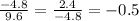
Now , formula of nth term in G.P. =
`f(n)=f(1)* r^(n-1)`

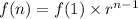
So, formula for nth term of the given sequence =
`f(n)=9.6* (-0.5)^(n-1)`

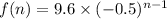
So,
`f(n-1)=9.6* (-0.5)^(n-1-1)`

`f(n-1)=9.6* (-0.5)^(n-2)`

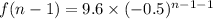
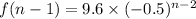
Recursive formula :

`(f(n))/(f(n-1))= (9.6* (-0.5)^(n-1))/(9.6* (-0.5)^(n-2))`

`(f(n))/(f(n-1))=(-0.5)^(n-1-(n-2))`

`(f(n))/(f(n-1))=(-0.5)^(-1+2)`

`(f(n))/(f(n-1))=-0.5`

`f(n)=-0.5* f(n-1)`

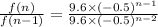
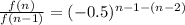
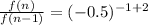
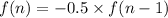
Hence recursive formula can be used to generate the sequence shown, where f(1) = 9.6 and n > 1 is
`f(n)=-0.5* f(n-1)`