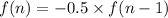Answer:
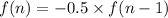
Explanation:
Sequence: 9.6, –4.8 , 2.4, –1.2, 0.6, ...
So, f(1) = first term = 9.6
r = common ratio =
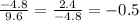
Now , formula of nth term in G.P. =
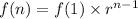
So, formula for nth term of the given sequence =
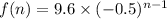
So,
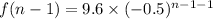
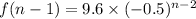
Recursive formula :
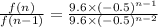
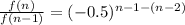
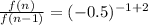
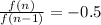
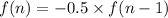
Hence recursive formula can be used to generate the sequence shown, where f(1) = 9.6 and n > 1 is