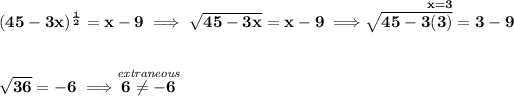Question

Can anyone help me with my algebra 2 semester 2 e2020 class? Specifically, the pretests for Adding and Subtracting Radicals, Multiplying Radicals, Dividing Radicals, and Radical Equations and Extraneous Roots?

Answer 1

Answer for adding and subtracting variables is is the pic.

Explanation:

Hope this helps!

Answer 2

`\bf (8x-8)^{(3)/(2)}=64~~ \begin{cases} 64=2\cdot 2\cdot 2\\ \qquad 2^3 \end{cases}\implies (8x-8)^{(3)/(2)}=2^3 \\\\\\ \textit{then we raise both sides by }(2)/(3)\implies \left[ (8x-8)^{(3)/(2)} \right]^{(2)/(3)}=(2^3)^{(2)/(3)} \\\\\\ (8x-8)^1=2^2\implies 8x-8=4\implies 8x=12 \\\\\\ x=\cfrac{12}{8}\implies x=\cfrac{3}{2}`


now onto the second one,



`\bf (45-3x)^{(1)/(2)}=x-9\impliedby \textit{we'll raise both by }^2 \\\\\\ \left[ (45-3x)^{(1)/(2)} \right]^2=(x-9)^2\implies (45-3x)^1=x^2-18x+81 \\\\\\ 45-3x=x^2-18x+81\implies 0=x^2-15x+36 \\\\\\ 0=(x-12)(x-3)\implies x= \begin{cases} 12\\ 3 \end{cases}`

now, the extraneous part, I don't see either as extraneous, 3 and 12 do work, however, I take it is referring to the root, so if we nevermind the root has ± versions, and say only assuming the value coming from the root is say positive, then


`\bf (45-3x)^{(1)/(2)}=x-9\implies √(45-3x)=x-9\implies \stackrel{x=3}{√(45-3(3))=3-9} \\\\\\ √(36)=-6\implies \stackrel{\textit{extraneous}}{6\\e -6}`