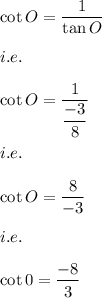Answer:
Hence, the answer is:
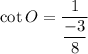 or
or
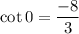
Explanation:
We know that the tangent trignometric function and the cotangent trignometric function is given by:
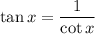
i.e. the tangent function and the cotangent function are inverse of each other.
We are given tangent of an angle O as:
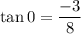
Hence, we have: