Question

Find the time, t, in seconds it takes for an object to fall from the top of a 1600 ft building by using the function h = -16^2 + 1600 (hint: set h=0).

Answer 1

The reason we set h equal to 0 is because h is height, and of course the height of an object when it is on the ground is 0. That looks like this then:
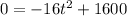
`0=-16t^2+1600`. To make this easier to factor, aka solving it for the time it takes to hit the ground, we will factor out a -16. That gives us this:
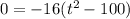
`0=-16(t^2-100)`. That means that, by the Zero Product Property, either -16=0, or
`t^2-100=0`. Of course
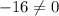
`-16 \\eq 0`, so that means that
`t^2-100=0`. We add 100 to both sides to get
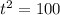
`t^2=100`. Taking the square root of both sides, t = -10 and t = 10. The 2 things in math that will never EVER be negative are time and distance/length, so that means that -10 seconds is out. Therefore, t = 10 seconds.