The reason we set h equal to 0 is because h is height, and of course the height of an object when it is on the ground is 0. That looks like this then:
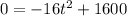
. To make this easier to factor, aka solving it for the time it takes to hit the ground, we will factor out a -16. That gives us this:
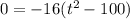
. That means that, by the Zero Product Property, either -16=0, or
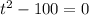
. Of course
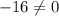
, so that means that
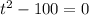
. We add 100 to both sides to get
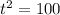
. Taking the square root of both sides, t = -10 and t = 10. The 2 things in math that will never EVER be negative are time and distance/length, so that means that -10 seconds is out. Therefore, t = 10 seconds.