Question

Diagram shows the composite solid formed by a cuboid and a right prism. Trapezium LMNP is the uniform cross section of the prism. It is given the volume of the composite solid is 444cm³. Calculate the length, in cm of MN​

Answer 1

MN = 7 cm

Explanation:

Well the volume we can separate into pieces

first the ABCDEFGH (? you know this cuboid)

which has a volume of

`V = AB\cdot BC\cdot CH\\\\V = 3*6*(3+JY+4)`

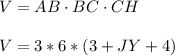
if you ask where does the 4 come from

it comes from LP = KB = YC and JY + YC =JC

so

`V = 18(7+MX)`

this is because JY = MX

the other volume is of BCNPKLXY (hope you understand which one)

and the volume is

`V = BP*PN*NX\\\\V=8*6*4\\\\V = 192`

and the last one is KYXLMJ (the top "triangle")

the volume is

`V = (LX*XM)/(2)*LK\\\\V = (6*MX)/(2)*8\\\\V= 6*4*MX\\\\V=24MX`

so now add them up

and has to equal 444

`V_T = 18(7+MX)+192+24MX\\\\V_T = 126+18MX+192+24MX\\\\V_T = 318+42MX\\\\444=318+42MX\\\\444-318=42MX\\\\126=42MX\\\\MX = 3`

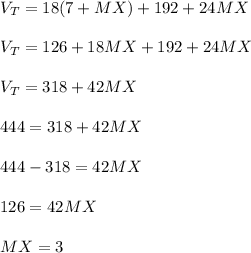
and finally we know that MN = MX + XN = 3+4 = 7

so here is our answer MN = 7 cm

a couple of notes

`1.\:\angle LXM = 90\\\\2.\:\angle KYX = 90`

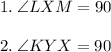
3. the units don't matter due to the fact that everything is in cm

4. see the picture below to get a better idea of which prism I am talking of

5. tell me if you have questions :D