Question

Charlene puts together two isosceles triangles so that they share a base, creating a kite. The legs of the triangles are 10 inches and 17 inches, respectively. If the length of the base for both triangles is 16 inches long, what is the length of the kite’s other diagonal?

Answer 1

We have to solve for the long diagonal.

Upper half of long diagonal^2 = 10^2 -8^2
Upper half of long diagonal^2 =100 -64
Upper half of long diagonal^2 =36

Upper half of long diagonal = 6



Lower Half of long diagonal^2 = 17^2 -8^2
Lower Half of long diagonal^2 = 289 -64
Lower Half of long diagonal^2 = 225


Lower Half of long diagonal = 15

Long Diagonal = 6 + 15 = 21 inches

Answer 2

The length of other diagonal of the kite is 21 inches.

Explanation:

Let the triangles are ADB and ACB, which share the same base AB,

Such that, AD = DB = 10 inches, AC = BC = 17 inches,

Also, the measure of their base = 16 inches,

⇒ AB = 16 inches

By making the diagram of this situation,

We get,

A kite ADBC,

Where, AB and DC are the diagonals,

We have to find : The measure of DC.

By the diagram, DC > AB,

DC is the major diagonal,

By the definition of kite, DC bisects AB perpendicularly,

Let O is the intersection point,

⇒ Δ AOC and Δ AOD are right triangles,

By the pythagoras theorem,

`AC^2=AO^2+OC^2\text{ and }AD^2=AO^2+OD^2`

`\implies OC=√(AC^2-AO^2)\text{ and }OD=√(AD^2-AO^2)`

`OC = √(17^2-8^2)\text{ and }OD=√(10^2-8^2)`

`OC=√(289-64)\text{ and }OD=√(100-64)`

`\implies OC=√(225)=15\text{ and }OD=√(36)=6`

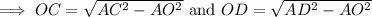
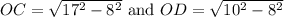
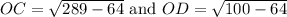
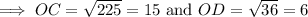
Hence, the measure of DC = OD + OC = 15 + 6 = 21 inches.