Answer:
The length of other diagonal of the kite is 21 inches.
Explanation:
Let the triangles are ADB and ACB, which share the same base AB,
Such that, AD = DB = 10 inches, AC = BC = 17 inches,
Also, the measure of their base = 16 inches,
⇒ AB = 16 inches
By making the diagram of this situation,
We get,
A kite ADBC,
Where, AB and DC are the diagonals,
We have to find : The measure of DC.
By the diagram, DC > AB,
DC is the major diagonal,
By the definition of kite, DC bisects AB perpendicularly,
Let O is the intersection point,
⇒ Δ AOC and Δ AOD are right triangles,
By the pythagoras theorem,
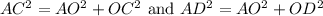
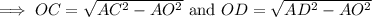
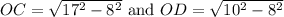
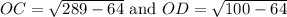
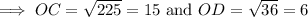
Hence, the measure of DC = OD + OC = 15 + 6 = 21 inches.