Question

A company makes and sells charm bracelets. The cost of producing x bracelets is represented by the function 

C(x) = 180 + 8x. The revenue earned from selling xbracelets is represented by the function R(x) = 20x. 
Write and simplify a function P that represents the profit made from selling x bracelets.
How many bracelets must the company sell to break even?

Answer 1

Profit is revenue minus cost.

P(x) = R(x) – C(x) or

P(x) = 20x – (180 + 8x)

Distribute and combine like terms.

P(x) = 12x – 180

The breakeven point is when P(x) = 0.

0 = 12x – 180

180 = 12x

x = 15

They must sell 15 bracelets to break even.

Answer 2

Profit is represented by revenue - cost. Therefore the function to find the profit would be
`P(x) = 20x - (180 + 8x)`.
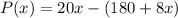
First, expand the - throughout the problem in the parenthesis.

`P(x) = 20x - 180 - 8x`
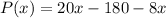
Combine like terms.

`P(x) = 12x - 180`
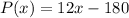
Now that we have our profit function, we need to find out how many need to be made to to break even. We can find this by setting the profit function to 0 and solving for x, since breaking even means they aren't making or losing profit.
Set P(x) to 0

`0 = 12x - 180`
Add 180 on both sides.

`180 = 12x`
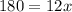
Divide by 12 on both sides.

`15 = x`
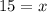
This means that the company will need to sell at least 15 bracelets to break even.