I assume that says
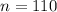
and
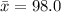
and
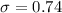
.
It doesn't really tell us if this is the standard deviation of the individual samples or of the sample average. Since they're related by a factor of
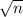
, around ten, some common sense tells us this is the standard deviation of the individual samples.
So we can conclude our sample mean has a standard deviation
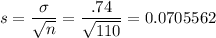
and that
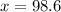
is

That's a huge z score, 8.5 standard deviations away. 110 is big enough we can just use the normal distribution and not worry about t distributions.
We can conclude the 98.6 is very unlikely to be the true mean or close to the true mean of human temperatures.