Question

To three decimal places, find the average value of f(x) = 2x2 + 3 on the interval [0, 2].

Answer 1

The formula for the average value of a function is
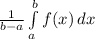
`(1)/(b-a) \int\limits^b_a {f(x)} \, dx` where b is the upper bound and a is the lower. For us, this formula will be filled in accordingly.
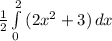
`(1)/(2) \int\limits^2_0 {(2x^2+3)} \, dx`. We will integrate that now:
`(1)/(2)[ (2x^3)/(3)+3x]` from 0 to 2. Filling in our upper and lower bounds we have
`(1)/(2)[( (2(2^3))/(3)+3(2))-0]` which simplifies to
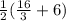
`(1)/(2)( (16)/(3)+6)` and
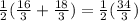
`(1)/(2)( (16)/(3)+ (18)/(3))= (1)/(2)( (34)/(3))` which is 17/3 or 5.667