The moon takes 28 days to orbit the earth at a distance of 240,000 miles. The satellite will take 24 hours to orbit the earth at an unknown distance.
We want to convert hours into days so that we have a constant unit of time for both the moon and satellite.
There are 24 hours in a day. Divide the amount of hours by 24:

The satellite will take 1 day to orbit the Earth.
This question involves Kepler's 3rd law of planetary motion. This law can use a simplified formula:
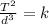
T is the orbital period, and d is the distance from the earth for the moon and satellite.
We can set k to equal the same formula:

Plug in your values for the moon and satellite:

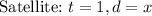

We can rearrange this proportion so that we can solve for x:
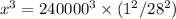
![\sqrt[3]{x^3} = \sqrt[3]{240000^3 * (1)/(784)}](https://img.qammunity.org/2019/formulas/physics/middle-school/6tfdr84v98iu2ifxnumyegrjbg8w0axekv.png)
![x = 240000 * \sqrt[3]{(1)/(784)}](https://img.qammunity.org/2019/formulas/physics/middle-school/2byes6hpmuq78pco2m1wcc52dhreso2cs5.png)
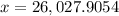
The altitude of this satellite will be
26,027.9 miles. Keeping significant figures in mind, the altitude will be
26,000 miles.