Question

Rex is currently taking physics as one of his electives in school. His grade at the end of the year is determined by the average of four exams, each worth 100 points. On his first test he got an 84, on his second he got a 86, and on his third an 92. What must he score on his fourth exam to get an A (90%) in the course?

A) 98
B) 90
C) 88
D) 86

Answer 1

The answer would be A)98.

I got this by taking the 3 test scores that were provided and adding them then subtracting that by 360 (90x4 - which would give you a 90 in the end) so I had 360 - 262 which equaled 98 and that would be the score needed to have a 90 in the end.

Answer 2

`\huge \bf༆ Answer ༄`

Total points is equal to :

`{ \qquad{ \sf{ \dashrightarrow}}}  \:  \: \sf \:100 * 4`

`{ \qquad{ \sf{ \dashrightarrow}}}  \:  \: \sf \:400 \: \: points`

90 % score is ~

`{ \qquad{ \sf{ \dashrightarrow}}}  \:  \: \sf \: (90)/(100) * 400`

`{ \qquad{ \sf{ \dashrightarrow}}}  \:  \: \sf \:90 * 4`

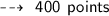
`{ \qquad{ \sf{ \dashrightarrow}}}  \:  \: \sf \:360 \: \: points`

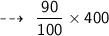
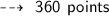
So, he has to get a total of 360 points to maintain 90% score.

let's assume his score in 4th test be ' x '

According to above conditions ~

`{ \qquad{ \sf{ \dashrightarrow}}}  \:  \: \sf \:x + 84 + 86 + 92 = 360`

`{ \qquad{ \sf{ \dashrightarrow}}}  \:  \: \sf \:x + 262 = 360`

`{ \qquad{ \sf{ \dashrightarrow}}}  \:  \: \sf \:x = 360 - 262`

`{ \qquad{ \sf{ \dashrightarrow}}}  \:  \: \sf \:x = 98`

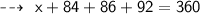
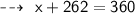
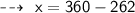
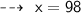
So, he must score 98 marks in the fourth test to achieve A (90%) in the course.