Question

For which discriminant is the graph possible?

b2 – 4ac = –12

b2 – 4ac = 0

b2 – 4ac = 7

Answer 1

discriminant must be minus cause the graph doesn't cross the x-axis .in other words it doesn't have an answer.plus , the "a" of the equation is minus too.

Answer 2

A)

`b^(2)-4ac=-12`

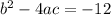
Explanation:

1) To answer this question, we must remember what this discriminant stands for:

`\Delta =b^(2)-4ac`

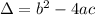
2) We must plug in this discriminant, in the square root of Quadratic Formula, to find its roots, i.e.:

`x=(-b\pm √(\Delta ))/(2a)`

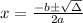
The discriminant is a radicand.

3) The graph above shows us no Real roots for this equation then we have roots ∈ Complex Numbers, in other words:

`x', x'' \in\:\mathbb{C}`

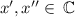
4) So, it's A.