Answer:
A)
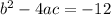
Explanation:
1) To answer this question, we must remember what this discriminant stands for:
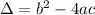
2) We must plug in this discriminant, in the square root of Quadratic Formula, to find its roots, i.e.:
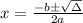
The discriminant is a radicand.
3) The graph above shows us no Real roots for this equation then we have roots ∈ Complex Numbers, in other words:
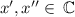
4) So, it's A.