Answer:
The time interval is
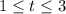 in which the height of the ball greater than or equal to 52 feet.
in which the height of the ball greater than or equal to 52 feet.
Step-by-step explanation:
We have given,When a baseball is hit by a batter, the height of the ball, h(t), at time t, t=0, is determined by the equation
 where t is time in seconds.
where t is time in seconds.
We have to find, If t is in seconds, for which interval of time is the height of the ball greater than or equal to 52 feet?
Solution :
The equation represented as

Where, t is time in seconds and h is the height.
We can solve the equation by putting h(t)=52

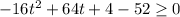
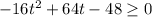
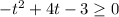
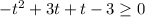
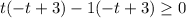
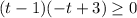
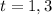
Therefore, The time interval is
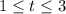 in which the height of the ball greater than or equal to 52 feet.
in which the height of the ball greater than or equal to 52 feet.
Now, We plot the graph of the given equation.
Refer the attached graph below.