Question

What is the simplified form of the following expression?

cube root of 4x/5

Answer 1

Answer:
`\frac{\sqrt[3]{100x}}{5}`

Step-by-step explanation:

Given expression : cube root of
`(4x)/(5)`

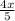
which is equivalent to
`\sqrt[3]{(4x)/(5)}`

To simplify this we need to make denominator a perfect cube.

So multiply and divide 25 inside the cube root, so that the denominator will become a perfect cube of 5.

`\sqrt[3]{(4x)/(5)}=\sqrt[3]{(4x)/(5)*(25)/(25)}\\=\sqrt[3]{(100x)/(125)}\\=\sqrt[3]{(100x)/(5^3)}\\=\frac{\sqrt[3]{100x}}{5}`

Answer 2

Answer:


`\frac{ \sqrt[3]{100x} }{5}`

Step-by-step explanation:


1) Given expression:


`\sqrt[3]{ (4x)/(5) }`

2) Multiply inside the root by 25 / 25


`\sqrt[3]{ (4x)/(5) (25)/(25) } = \sqrt[3]{ (100x)/(125) }= \frac{ \sqrt[3]{100x} }{5}`