Answer:
![\frac{\sqrt[3]{100x}}{5}](https://img.qammunity.org/2019/formulas/mathematics/high-school/am22hesiihoq6a5hgf6zne4ff4wxicv1wo.png)
Step-by-step explanation:
Given expression : cube root of
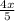
which is equivalent to
![\sqrt[3]{(4x)/(5)}](https://img.qammunity.org/2019/formulas/mathematics/high-school/t4aswmw45jcfz5rn5y9ggmyxsknnilnd1c.png)
To simplify this we need to make denominator a perfect cube.
So multiply and divide 25 inside the cube root, so that the denominator will become a perfect cube of 5.
![\sqrt[3]{(4x)/(5)}=\sqrt[3]{(4x)/(5)*(25)/(25)}\\=\sqrt[3]{(100x)/(125)}\\=\sqrt[3]{(100x)/(5^3)}\\=\frac{\sqrt[3]{100x}}{5}](https://img.qammunity.org/2019/formulas/mathematics/high-school/1qe8lvmr4jvf8s4hwcpvtd89uyw59xcqed.png)