Question

Let f(x)=e^x and g(x)=x-3 what are the domain and range of (f g) (x)

A. domain: x>0 range: y<0
B. domain: x>3 range y>0
C. domain: al real numbers range: y<0
D. domain: all real numbers range: y>0

Answer 1

D. Domain: all rea numbers

Range: y >0

Explanation:

Let f(x) =
`e^x`

Domain of function f(x) : all real numbers because it is define for every real number.

Range of function f(x) y >0 because exponential function can never be zero.

g(x)=x-3

Domain of g(x) : all real numbers

Range g(x): all real numbers.

(fg)(x)= f(g(x))

f(x-3)=
`e^(x-3)`

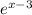
(fg)(x)=
`e^(x-3)`

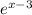
Put x=0 then we get

`(fg)(0)= [tex]e^(0-3)`

(fg)(0)=
`e^(-3)`

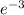
Domain of (fg)(x) is the set of real numbers because it is define for every real number.

Exponential function can never be zero .

Function (fg)(x) can never be zero it is always greater than zero because it is an exponential function

Therefore , the range of (fg)(x) is greater than zero.

Hence, option D is correct .

Domain: all real numbers

Range: y >0

Answer 2

The domain and range of g are "all real numbers," so you want to find the range of f when its argument is from the set "all real numbers." That range is y > 0. The appropriate choice is
D. domain: all real numbers; range: y > 0