Answer:
D. Domain: all rea numbers
Range: y >0
Explanation:
Let f(x) =
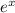
Domain of function f(x) : all real numbers because it is define for every real number.
Range of function f(x) y >0 because exponential function can never be zero.
g(x)=x-3
Domain of g(x) : all real numbers
Range g(x): all real numbers.
(fg)(x)= f(g(x))
f(x-3)=
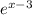
(fg)(x)=
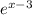
Put x=0 then we get
![(fg)(0)= [tex]e^(0-3)](https://img.qammunity.org/2019/formulas/mathematics/high-school/5rx0l0gskuc6z31gruyz5ym51mx0e0mzi3.png)
(fg)(0)=
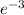
Domain of (fg)(x) is the set of real numbers because it is define for every real number.
Exponential function can never be zero .
Function (fg)(x) can never be zero it is always greater than zero because it is an exponential function
Therefore , the range of (fg)(x) is greater than zero.
Hence, option D is correct .
Domain: all real numbers
Range: y >0