To make this as easy as possible, we will find the vertex from the equation above. The vertex is sitting at (h, k) of (2, -3). The directrix is the same number of units from the vertex that the focus is. The formula for the focus for an upwards-opening parabola is
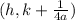
. The "a" in that formula is the 1/4 sitting in front of (y+3). Filling in accordingly, we have
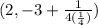
. Simplifying we get

. The focus is on the axis of symmetry along with the vertex, and is 1 unit above the vertex. That means that the directrix is 1 unit BELOW the vertex and is a horizontal line. Therefore, the directrix has an equation of y = -4