The correct answer is option #1. x = -2 +/- 2i
We can find this by using the quadratic equation, which is written below.
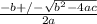
Now we know the a, b and c values by looking at the equation. a is always the number attached to x^2 (which is 1), b is always the number attached to x (which is 4) and c is the number with no variable (which is 8). So we can place them in in the appropriate spots in the equation.
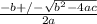
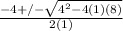
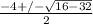
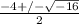
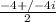
-2 +/- 2i