Answer: The y co-ordinate of the point L is -11.
Step-by-step explanation: Given that the co-ordinates of the endpoints of the line segment JK are J(–25, 10) and K(5, –20).
We are to find the y co-ordinate of he point L that divides the line segment JK in the ratio 7 : 3.
We know that
the co-ordinates of a point that divides the line segment with endpoints (a, b) and (c, d) in the ratio m : n are given by

Therefore, the y co-ordinate of the point L will be
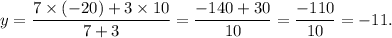
Thus, the y co-ordinate of the point L is -11.