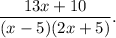Question

Simplify (3/2x+5)+(5/x-5)

A. 15x+5/(x-5)(2x+5)

B. 15/(x-5)(2x+5)

C. 10x+12/6(x-6)

D. 13x+10/(x-5)(2x+5)

Answer 1

`\bf \cfrac{3}{2x+5}+\cfrac{5}{x-5}\impliedby \stackrel{LCD}{(2x+5)(x-5)}\implies \cfrac{3(x-5)~~+~~5(2x+5)}{(2x+5)(x-5)} \\\\\\ \cfrac{3x-15~~+~~10x+25}{(2x+5)(x-5)}\implies \cfrac{13x+10}{(2x+5)(x-5)}`

Answer 2

Answer: The required simplified form of the given expression is
`(13x+10)/((x-5)(2x+5)).`

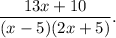
Step-by-step explanation: We are given to simplify the following expression :

`E=(3)/(2x+5)+(5)/(x-5)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

To simplify the given expression, we need to take the lcm of the denominators first.

The simplification of expression (i) is as follows :

`E\\\\\\=(3)/(2x+5)+(5)/(x-5)\\\\\\=(3(x-5)+5(2x+5))/((2x+5)(x-5))\\\\\\=(3x-15+10x+25)/((x-5)(2x+5))\\\\\\=(13x+10)/((x-5)(2x+5))\\`

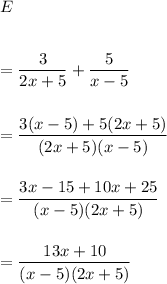
Thus, the required simplified form of the given expression is
`(13x+10)/((x-5)(2x+5)).`