Question

One x-intercept for a parabola is at the point (4,0). Find the other x-intercept for the parabola defined by this equation y=x^2-x-12

Answer 1

Probably the easiest way to do this is to use synthetic division. We already know one of the zeros of the quadratic so we can use that number to find the other zero. If the point is (4, 0), then when y = 0, x = 4. Thus, 4 is a zero. Put 4 outside the "box" and put the coefficients from the quadratic inside, like this: 4 (1 -1 -12). Draw a line and bring down the first one under it. Multiply that 1 by the 4 to get 4. Put that 4 up under the -1 and add to get 3. Multiply 3 by 4 to get 12. Put that 12 up under the -12 and add to get 0. The numbers left under the line are the coefficients for the next polynomial, called the depressed polynomial, and this polyomial is one degree less than the one we started with. Those coefficients are 1 and 3. Therefore, the polynomial is x + 3 = 0. That means that the other zero, or x-intercept, is x = -3.

Answer 2

(-3,0)

Explanation:

Hello!

The average of the two x-values of the x-intercepts is the Axis of Symmetry of a parabola. The formula for the axis of symmetry is
`(-b)/(2a)`.

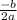Given the standard form of a quadratic is
`ax^2 + bx + c` and our equation
`x^2 - x - 12`:

Solve for the AOS:

• 
  `x^2 - x - 12\\`
• 
  `(-(-1))/(2(1))`
• 
  `\frac12`

To solve for the other x-intercept:

Find the missing value so that when added to 4 and divided by 2, you get 1/2

• 
  `(4 + x)/(2) = \frac12`
• 
  `4 + x = 1`
• 
  `x = -3`

The missing x-intercept is (-3,0)