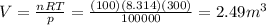We can solve the problem by using the ideal gas equation:
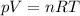
where
p is the pressure of the gas
V is the volume of the gas
n is the number of moles of the gas
R is the gas constant
T is the absolute temperature of the gas
For the gas in our problem, we have:
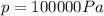
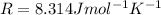
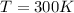
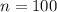
If we rearrange the equation and we put these numbers into it, we find the volume of the gas: