Question

Equilateral triangle mnp has perimeter 12a+18b. line segment qr is a midsegment. what is qr?

Answer 1

Let the triangle be abc with equal sides ab,bc and ca
then perimeter = 3 ab = 12a + 18b

ab = = 4a + 6b ( each side will have this length)

Now since qr is a mid segment it will be = half length of ab

So qr = 2a + 3b Answer

Answer 2

qr = 2a + 3b

Explanation:

First, we must calculate the measure of each side based on the perimeter. Since all three sides of an equilateral triangle are equal, we divide the perimeter by 3.

`(12a+18b)/(3)`

`(12a)/(3)+(18b)/(3)`

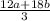
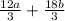
4a + 6b (measure of each side)

Being an equilateral triangle, any middle segment is half the length of any of its sides.

So, the value of qr is:

`qr = (4a+6b)/(2)\\qr = (4a)/(2) + (6b)/(2) \\qr = 2a + 3b`

---------------------------------------------------------------------------

Hope this hepls!