Question

Find the values of k so that each remainder is three.
10. (x^2+ 5x + 7) = (x + k)

Answer 1

`k=1\text{ or } k=4`

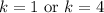
Explanation:

We can use the Polynomial Remainder Theorem. It states that if we divide a polynomial P(x) by a binomial in the form (x - a), then our remainder will be P(a).

We are dividing:

`(x^2+5x+7)/(x+k)`

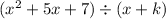
So, a polynomial by a binomial factor.

Our factor is (x + k) or (x - (-k)). Using the form (x - a), our a = -k.

We want our remainder to be 3. So, P(a)=P(-k)=3.

Therefore:

`(-k)^2+5(-k)+7=3`

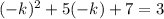
Simplify:

`k^2-5k+7=3`

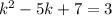
Solve for k. Subtract 3 from both sides:

`k^2-5k+4=0`

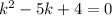
Factor:

`(k-1)(k-4)=0`

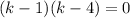
Zero Product Property:

`k-1=0\text{ or } k-4=0`

Solve:

`k=1\text{ or } k=4`

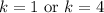
So, either of the two expressions:

`(x^2+5x+7)/(x+1)\text{ or } (x^2+5x+7)/(x+4)`

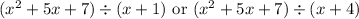
Will yield 3 as the remainder.