Question

Please Help!!! Which Of the following is the minium value of the function


`y = (3)/(4) x ^(2) + 6x + 6`
A. -6

B. 3/4

C. -4

D. 6

Answer 1

Begin by setting the equation = to 0, and then move the 6 over by subtraction. Here's what it is now:
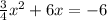
`(3)/(4) x^(2) +6x=-6`. Now we are ready to complete the square on the x terms. First, though, the rule is that the leading coefficient has to be a +1. Ours is a 3/4. So we will factor it out. When we do that, we get
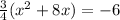
`(3)/(4) ( x^(2) +8x)=-6`. Take half the linear term, square it and add it to both sides. Our linear term is 8. Half of 8 is 4, and 4 squared is 16. So add 16 to the left inside the parethesis...BUT don't forget about that 3/4 out front there, refusing to be ignored. It is a multiplier. So what we have really added in is (3/4)(16), which is 12. Now here's what we have:
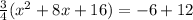
`(3)/(4)( x^(2) +8x+16)=-6+12`. Simplifying the right side we have
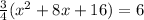
`(3)/(4) ( x^(2) +8x+16)=6`. The whole point of this is to create a perfect square binomial on the left which will serve as the h in our vertex (the x-coordinate). That binomial is this:
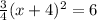
`(3)/(4) (x+4)^2=6`. Now we will move the 6 back over by subtraction and set it back equal to y.
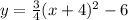
`y= (3)/(4) (x+4)^2-6`. The minimum value is reflected in the k value of the vertex (the y-coordinate), which is -6. So our answer is A from above.