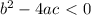By definition, the roots of a quadratic function can be found using an equation of the form:
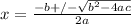
The discriminant is the following part of the expression:
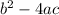
Therefore, we have three cases:
Case 1:
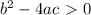
Then there are two real solutions
Case 2:
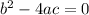
Then there is a real solution with multiplicity two
Case 3:
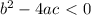
There are no real solutions
When the graph of a quadratic equation has no cut points with the x axis, then we are in case number 3.
Answer:
B. Negative