Question

Question 1(Multiple Choice Worth 2 points)

Use the given graph to determine the limit, if it exists.

A coordinate graph is shown with a downward sloped line crossing the y axis at two that ends at the open point 2, 1.3, a closed point at 2, -1, and an upward sloped line starting at the open point 2, 4.

Find = limit as x approaches two from the right of f of x..

1.3
4
-1
5

Question 2(Multiple Choice Worth 4 points)

Use the given graph to determine the limit, if it exists.

A coordinate graph is shown with a horizontal line crossing the y axis at three that ends at the open point 2, 3, a closed point at 2, 1, and another horizontal line starting at the open point 2, -3.

Find limit as x approaches two from the left of f of x. and limit as x approaches two from the right of f of x..

1; 1
3; -3
Does not exist; does not exist
-3; 3

Question 3 (Essay Worth 4 points)

Use the given graph to determine the limit, if it exists.

A coordinate graph is shown with a downward sloped line crossing the y axis at the origin that ends at the open point 3, -1, a closed point at 3, 7, and a horizontal line starting at the open point 3, -4.

Find limit as x approaches three from the left of f of x..

Answer 1

These are 3 questions and 3 answers.

1) Find



`\lim_(x \to \ 2^+) f(x)`

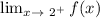Answer: 4.

Step-by-step explanation:

The expression means the limit as the function f(x) approaches 2 from the right.

Then, you have to use the function (the line) that comes from the right of 2 and gets as close as you want to x = 2.

That is the line that has the open circle around y = 4, and that is the limit searched.

2) Use the graph to determine the limit if it exists.

Answer:


`\lim_(x \to \ 2^-) f(x) = 3`


`\lim_(x \to \ 2^+) f(x)=-3`

To determine each limit you use the function from the side the value of x is being approached.

Note, that since the two limits are different it is said that the limit of the function as it approaches 2 does not exist.

3)
Answer: - 1



`\lim_(x \to \ 3^-) f(x) = -1`

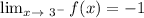
To find the limit when the function is approached to 3 from the left you follow the line that ends with the open circle at (3, -1).

Therefore, the limit is - 1.