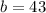Answer:
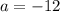 and
and
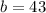
Explanation:
To find the constants, we need to replace the given point
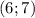 into the given quadratic function:
into the given quadratic function:

So, from the problem we have
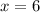 and
and
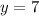 . Then:
. Then:
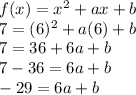
However, if we have a minimum at
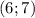 , the first derivate of the function must be zero at 6.
, the first derivate of the function must be zero at 6.
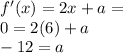
Now, we substitute this value in the previous expression:
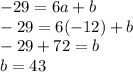
Therefore, the values of the constants are
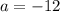 and
and