Question

The length of a rectangle is 1 less than twice the width. The area of the rectangle is 28 square feet.What is the length of the rectangle?

Answer 1

We need to use that first sentence to get the length in terms of the width because you can't have more than 1 unknown in a single equation without running into impossible problems. Putting those words into a usable, viable equation, gives us L = 2w - 1. That's the length that is 1 less than twice the width. The width is just w. Area then requires that we multiply the length and the width together. We have an area of 28, so here's what that looks like:
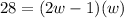
`28=(2w-1)(w)`. Distribute the right side to get
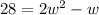
`28=2w^2-w`. Now, set the equation equal to 0 and bring the 28 over to the other side by subtraction so we can factor the polynomial.
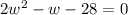
`2w^2-w-28=0`. Factor that best by putting those values into the quadratic formula to get that w = 4 and w = -3.5. We know, however, that the 2 things in math that will never EVER be negative are time and distance/length, so -3.5 is out. That means that the width is 4. The length equation, remember, is L = 2w-1, so L=2(4)-1 which is 8-1 = 7. The width is 4 and the length is 7.

Answer 2

Length = 7 feet .

Explanation:

Given : The length of a rectangle is 1 less than twice the width. The area of the rectangle is 28 square feet.

To find : .What is the length of the rectangle.

Solution : we have given that

Let the length of rectangle = L

Width = w

According to question :

The length of a rectangle is 1 less than twice the width.

L = 2 w - 1 .

Area = length * width .

Area = L * w .

Plug the values

28 = (2w -1) * w.

28 = 2w² - w.

On subtracting 28 from both sides

2w² - w - 28 = 0.

On factoring

2w² -8w + 7w - 28 = 0.

2w ( w - 4) +7( w - 4) = 0.

On grouping

( 2w + 7) ( w -4) = 0

For

w -4 = 0 or 2w + 7 = 0

w = 4 or w = - 3.7

Width can not be negative so we ignore w =-3.5.

So , width = 4 feet.

Length (L) = 2w -1

L = 2(4) -1

L = 8 -1

L = 7 feet

Therefore, Length = 7 feet .