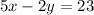Question

Find the equation in standard form of the line passing through the points (3,-4) and (5,1)

Answer 1

Answer:
`5x-2y=23`

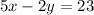
Explanation:

The equation of a line passing through (a,b) and (c,d) is given by :-

`(y-b)=(d-b)/(c-a)(x-a)`

Also , the equation of a line in standard form is given by :-

`Ax+By=C`

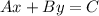
Then , the equation of a line passing through points (3,-4) and (5,1) will be :-

`(y-1)=(-4-1)/(3-5)(x-5)`

`\Rightarrow\ (y-1)=(-5)/(-2)(x-5)`

`\Rightarrow\ (y-1)=(5)/(2)(x-5)`

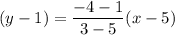
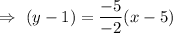
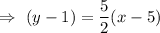
Convert into standard form.

`\Rightarrow\ 2(y-1)=5(x-5)`

`\Rightarrow\ 2y-2=5x-25`

`\Rightarrow\ 25-2=5x-2y`

`\Rightarrow\ 5x-2y=23`

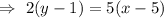
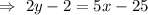
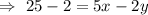
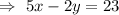
Hence, the standard form of the line passing through the points (3,-4) and (5,1) :
`5x-2y=23`

Answer 2

5x-2y=23

Explanation:

The line is passing through the points (3,-4) and (5,1).

Thus, we have

`x_1=3,y_1=-4,x_2=5,y_2=1`

The slope of the line is given by

`m=(y_2-y_1)/(x_2-x_1)\\\\m=(1+4)/(5-3)\\\\m=(5)/(2)`

The point slope form of a line is given by

`y-y_1=m(x-x_1)\\\\y+4=(5)/(2)(x-3)\\\\y+4=(5)/(2)x-(15)/(2)\\\\2y+8=5x-15\\\\5x-2y=23`

Thus, the standard form of the line is given by 5x-2y=23