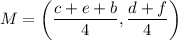Question

Click an item in the list or group of pictures at the bottom of the problem and, holding the button down, drag it into the correct position in the answer box. Release your mouse button when the item is place. If you change your mind, drag the item to the trashcan. Click the trashcan to clear all your answers. Prove: The segments joining the midpoints of the opposite sides of a quadrilateral bisect each other. Midpoints of both segments are the same point; therefore, segments bisect each other.

Answer 1

All you need to do is copy the letters and numbers from the figure for R, S, T, and U. It is as easy to do that as it is to copy from my answer here. For example,
R = (b/2, 0)

The point M is the midpoint of both SU and RT. Since it comes out the same either way, it doesn't matter which pair of points you use to find M. However, the "b+c+" in the first expression x-coordinate suggests you start with point S.


`M=(S+U)/(2)=\left((\left((b+c)/(2)\right)+\left((e)/(2)\right))/(2),(\left((d)/(2)\right)+\left((f)/(2)\right))/(2)\right)\\\\M=\left((b+c+e)/(4),(d+f)/(4)\right)`

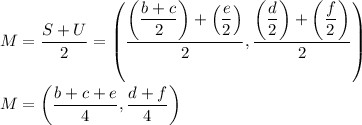
Then the other expression for M will fill in as ...


`M=\left((c+e+b)/(4),(d+f)/(4)\right)`