The complete problem is as following:
A train traveling at a constant speed takes a passenger from Elm to Millwood, stopping at Centre along the way. It takes 5 times as long to go from Centre to Millwood as it does to go from Elm to Centre. The entire trip is 48 miles. How far is the ride from Centre to Millwood? Name a geometric postulate or theorem used to find the solution.
A) 8 miles ; segment addition postulate
B) 8 miles; segment bisector theorem
C) 40 miles; segment addition postulate
D) 40 miles; segment bisector theorem
=======================================================
Solution ;
Let the time taken from Elm to Centre = x ⇒⇒⇒ segment (1)
∴ the time taken from Centre to Millwood = 5x ⇒⇒⇒ segment (2)
∴ Total time of all the trip = x + 5x = 6x
The entire trip is 48 miles and the train traveling with constant speed
∴ speed = distance over the time =
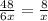
So, the distance from Centre to Millwood = speed * time =
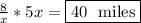
As seen in the answer, we have added the segment (1) to segment (2)
So, The geometric postulate used to find the solution is segment addition postulate
So, the correct option is C) 40 miles; segment addition postulate
=======================================================
Another solution :
From Elm to Centre = x ⇒⇒⇒ segment (1)
From Centre to Millwood = 5x ⇒⇒⇒ segment (2)
∵ The train traveling with constant speed
∴ Distance is proportional with the time
By using the ratio and proportional as following
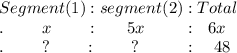
∴ segment (2) =
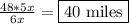
we have used the postulate of segment addition to add x and 5x.
So, the correct option is C) 40 miles; segment addition postulate