Question

The function f(x) = x + is used to complete this table.

x: -1, 0, 1, 2 f(x): 1, 3/2, 2, 5/2

Which statements are true of the given function? Check all that apply.
f(-1/2)= -2
f(0)= 3/2
f(1)= -1
f(2)= 1
f(4)= 7/2

Answer 1

The answer is B. and E. the only fractions on there

Explanation:

Answer 2

The first thing we must do for this case is to identify the function that models the table.We have a function of the form:

`f (x) = mx + b`
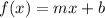
Where,
m: slope of the line
b: cutting point with the y axis
We observe that for x = 0 the value of the function is f (0) = 3/2. From here, it is concluded:

`b = 3/2`
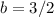
Then, the change of rate is constant and equal to 1/2, therefore,

`m = 1/2`
So, the function is:

`f (x) = (1/2) x + 3/2`
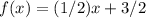
Therefore, we have:

`f (-1/2) = (1/2) (- 1/2) + 3/2 = 5/4 f (0) = (1/2) (0) + 3/2 = 3/2`

`f (1) = ((1/2) (1) + 3/2 = 2 f (2) = (1/2) (2) + 3/2 = 5/2 f (4) = (1/2) (4) + 3/2 = 7/2`
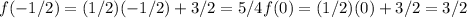
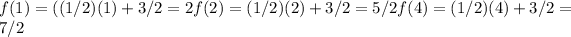Answer:
statements that are true of the given function:

`f (0) = 3/2 f (4) = 7/2`