Answer:
The graph of given function is shown below.
Explanation:
The given function is
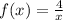
We need top find the graph of given rational function.
First find the key features of the given function.
1. Vertical asymptote: Equate denominator equal to 0.

The vertical asymptote is x=0.
2. Horizontal asymptote: Find the
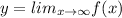 to find the horizontal asymptote.
to find the horizontal asymptote.
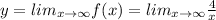
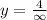
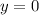
The horizontal asymptote is y=0.
3. The graph has vertical asymptote is x=0 and horizontal asymptote is y=0, therefore the graph has no x- and y-intercepts.
4. End behavior:
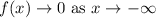
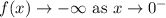
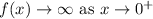

5. Table of value:
The table of values is
x f(x)
-2 -2
-1 -4
1 4
2 2
Plot these ordered pairs on a coordinate and connect these points by free hand curve using the key features.