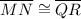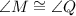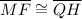Answer:
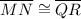
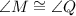
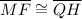
Explanation:
We know that if two triangles are congruent , then the corresponding angles and sides are congruent by CPCTC.
Given:
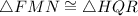
Therefore , the corresponding angles and sides of
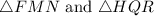 are congruent.
are congruent.
∠F corresponds ∠H
∠M corresponds ∠Q
∠N corresponds ∠R
⇒ ∠F ≅ ∠H
∠M ≅ ∠Q
∠N ≅ ∠R
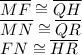
So , from the given options, the true congruency statements are :-